Stetigkeit

Stetigkeit ist das zentrale Konzept in der Analysis. Über stetige Funktionen kann man enorm viele Aussagen treffen.

Was bedeutet aber Stetigkeit eigentlich?

Ganz einfach und anschaulich gesprochen: eine Funktion ist stetig, wenn sie mit einem Stift ohne abzusetzen zu zeichnen ist. Die Funktion hat also keine Sprünge oder so etwas. Hier seht ihr eine stetige und eine unstetige Funktion:

So weit so einfach. Deutlich komplizierter wird es, wenn man sich die tatsächliche mathematische Definition dieser Aussage anschaut. Wenn man darüber nachdenkt, sollte klar sein, dass sich die Aussage mit dem Stift nicht so einfach in eine Formel übertragen lässt. Tatsächlich tut die folgende Formel – auch wenn sie sehr kompliziert aussieht – genau das! Die Idee ist im Prinzip folgende: Wenn eine Funktion ohne Abzusetzen zeichenbar ist, bedeutet das, wenn ich mit dem Stift die Funktion zeichnen will, und nur ein kleines Stück in x-Richtung gehe, dann sollte ich auch nur ein verhältnismäßig kleines Stück in y-Richtung gehen müssen. Dann ist die Funktion stetig. Bei unstetigen Funktionen, wo die Funktion zum Beispiel einen Sprung nach unten macht, wie z.B. die rote aus dem Bild oben, gibt es nun aber Stellen, wo ich nur ein kleines Stück in x-Richtung gehe, aber auf einmal eben einen ganz schönen Sprung in y-Richtung machen muss. Das ist dann nicht mehr stetig.

Schauen wir uns nun also die Definition an, aber nicht erschrecken! Später gibt es noch ein metaphorisches Beispiel, was das eigentlich ganz anschaulich macht.

Definition: Stetigkeit (auch: Epsilon-Delta-Kriterium)

Eine Funktion $f : D \rightarrow \mathbb{R}$ ist stetig im Punkt p, wenn dort gilt: Zu jedem $\varepsilon > 0$ existiert ein $\delta>0$ sodass für alle $x$ mit $\left| x-p \right|<\delta $ folgt, dass $ \left| f(x) – f(p) \right| < \varepsilon$ gilt. Wenn $f$ in jedem Punkt $p \in D$ stetig ist, so ist eben die ganze Funktion $f$ stetig.

Sieht erstmal ziemlich komisch aus, oder? Brechen wir diese Definition einmal herunter: Zu jedem Epsilon, also zu jeder Änderung in y-Richtung existiert (mindestens!) ein Delta, also eine Änderung in x-Richtung, sodass bei jeder Veränderung von p um weniger als Delta, die Funktion nicht weiter als Epsilon vom Wert f(p) abhaut. Folgende Darstellung veranschaulicht dies ein bisschen, zu der Epsilon-Umgebung um f(p) finden wir eine Delta-Umgebung von p.

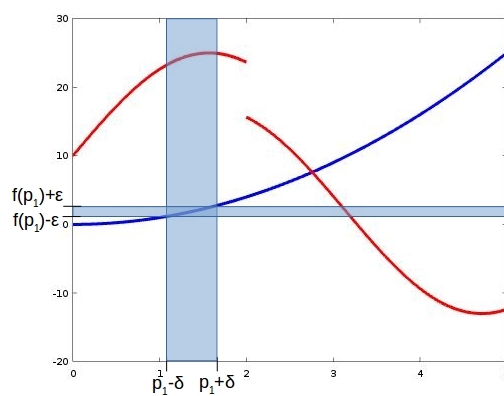
Das dies wirklich zeigt, dass eine Funktion stetig ist, sollte das folgende metaphorische Beispiel klar machen:

Die unstetige Dusche

Es geht um unsere morgendliche Dusche! Und zwar so: die x-Werte beschreiben die Position des Wärme-Reglers, die y-Werte die Temperatur des Duschwassers. Wenn wir die Temperatur stetig verändern können, bedeutet das folgendes: Zu jeder (auch noch so kleinen) Änderung Epsilon der Temperatur (Änderung in y-Richtung) gibt es eine Veränderung Delta der Position des Wärme-Reglers (in x-Richtung), sodass eine Veränderung des Reglers um maximal Delta auch nur eine Veränderung der Temperatur um maximal Epsilon bewirkt.

Wenn unsere Dusche jetzt nicht stetig wäre, sagen wir, sie springt von 20° auf 40° (kennt jeder, unglaublich nervig), finden wir zu bestimmten Epsilons eben kein passendes Delta:
Sagen wir, unser Regler hat gerade die Position p und die Dusche ist 20° warm. Das bedeutet nun, wir finden absolut kein Delta, sodass wir den Regler um dieses Delta drehen, damit die Temperatur auf 30° steigt! Zu einer Änderung um diese 10° in y-Richtung gibt es einfach kein Delta, sodass eine Veränderung in x-Richtung die y-Werte nur um 10° verändern lässt. Mathematisch ausgedrückt: Für $\varepsilon = 10$ existiert an der Stelle p kein $\delta>0$ sodass aus $\left| x-p \right|<\delta$ die Aussage $\left| f(x) – f(p) \right|<10$ folgt. Egal wie sanft wir den Regler bewegen: kaaalt, kaalt, kaaalt, kaaalt, HEISS HEISS HEISS!! Es gibt nichts dazwischen. Die Funktion ist nicht stetig. Wir geben auf und duschen kalt. Ist eh besser für die Umwelt und macht uns wach um jetzt Stetigkeit anhand von Beispielen zu bestimmen!

Epsilon-Delta-Kriterium für Stetigkeit am Beispiel

Lasst uns das Epsilon-Delta-Kriterium einmal an ein paar Beispielen durchrechnen!
Beginnen wir mit der Funktion $x^2$. Schauen wir mal, ob diese Funktion in p=0 stetig ist. Es ist also folgendes zu zeigen:
Für alle $\varepsilon>0$ müssen wir immer mindestens ein $\delta>0$ finden, sodass gilt:
$$ \left| x-0 \right| < \delta \Rightarrow \left| f(x) – f(0) \right| < \varepsilon $$

Das funktioniert folgendermaßen: Man beginnt mit dem Term $ \left| f(x) – f(p) \right|$ und versucht ihn so umzubiegen, dass dort irgendetwas mit $\left| x-p \right|$ steht. Dann kann herausfinden, wie das Delta in Abhängigkeit von Epsilon, x und p gewählt werden kann, um die Stetigkeit zu beweisen. Beim Umbiegen darf muss man aber immer kleiner als $\varepsilon$ bleiben, das heißt jede Umformung ist eine Gleichheit, oder man wird noch kleiner. (Dazu in Beispiel 3 mehr!)
Hier ist also:
$\left| f(x) – f(0) \right| = \left| x^2 – 0 \right| = \left| (x-0)(x-0) \right| = \left| x-0 \right|^2 $.
Das soll nun kleiner als $\varepsilon$ sein. Naja, und wenn das $< \varepsilon$ sein soll, dann muss offenbar $\left| x-0 \right|$ kleiner als $\sqrt{\varepsilon}$ sein.
Damit haben wir also zu JEDEM $\varepsilon$ ein $\delta$ gefunden, sodass gilt:
$\left| x-p \right|<\delta \Rightarrow \left| f(x) – f(p) \right|<\varepsilon$, denn aus $ \left| x-0 \right| < \sqrt{\varepsilon}$ folgt $\left| f(x) – f(0) \right| < \varepsilon$

Zweites Beispiel für Stetigkeit

Gleiche Funktion, diesmal p=1.
WIr fangen wieder mit $|f(x) – f(p)|$ an und versuchen, etwas mit $|x-p|$ daraus zu machen:
$$ \left| f(x) – f(1) \right| = \left| x^2 – 1 \right| = \left| (x-1)(x+1) \right| = \left| x-1 \right| ~ \left| x+1 \right| $$
Wenn also  $\left| f(x) – f(1) \right| < \varepsilon$ sein soll, dann ist also $\left| x-1 \right| ~ \left| x+1 \right| < \varepsilon$ und damit können wir $\delta = \frac{\varepsilon}{\left| x+1 \right|}$ wählen.
Denn: $\left| x-1 \right| < \frac{\varepsilon}{\left| x+1 \right|} \Rightarrow \left| f(x) – f(1) \right| = \left| x-1 \right| ~ \left| x+1 \right| < \frac{\varepsilon}{\left| x+1 \right|}\left| x+1 \right| = \varepsilon$ und die Stetigkeit ist gezeigt.

Ein Beispiel einer nicht-stetigen Funktion

$$f(x) =  \begin{cases} \frac{x^2-1}{x-1} & x \neq 1 \\ 1 & x=1 \end{cases} $$

Ist diese Funktion stetig in p=1?

Wir beginnen wie immer:
$$\left| f(x) – f(1) \right| = \left| \frac{x^2-1}{x-1} – 1 \right| = \left| \frac{(x-1)(x+1)}{x-1} – 1 \right| = \left| (x+1) – 1 \right| = \left| x \right|$$
Wir müssen also $\delta$ finden, sodass für jedes $\epsilon>0$ gilt: $||x-1|<\delta \Rightarrow |x|<\varepsilon$.
Aber geht das überhaupt?
Wenn zum Beispiel $\varepsilon = 1,5$, dann geht das: Für jedes $\delta < 0.5$ wäre dann tatsächlich $|x| < 1,5$.
Aber das muss für jedes $\varepsilon$ gelten!
Wenn $\varepsilon = 0,2$, dann finden wir absolut kein $\delta$, sodass für alle x mit $|x-1|<\delta$ folgt, dass $|x|<0,5$.
Zu diesem Epsilon gibt es also schlicht und ergreifend kein passendes Delta! Bei jedem Delta werden einige x-Werte die Bedingung nicht erfüllen! Die Funktion ist nicht stetig.
In der folgenden Graphik ist sind nochmal die beiden Epsilons eingezeichnet: Für $\varepsilon = 1,5$ finden wir ein Delta, sodass alle x die im grünen Bereich liegen ($|x|<\delta$) auch in $|x-1|<\varepsilon$ liegen. Dort gilt also $|x-1|<\delta \Rightarrow \left| f(x)-f(1) \right|<1,5$. Es muss aber für jedes Epsilon gelten. und egal wie wir unser Delta wählen, für $\epsilon_2$ werden immer einige x-Werte außerhalb der Epsilon-Umgebung (rot) liegen.

Das war es erst einmal zum Epsilon-Delta Kriterium der Stetigkeit! Es gibt auch noch weitere Kriterien der Stetigkeit, die ich euch auch bald zeigen werde. Also schaut regelmäßig vorbei!