Komplexe Zahlen: Grundlagen

Was sind komplexe Zahlen und wofür braucht man sie?

Komplexe Zahlen sind eine Erweiterung der reellen Zahlen. Sie sind ein Zahlensystem, welches die reellen Zahlen enthält, aber auch noch mehr. Wozu braucht man so etwas? Nun, neue Zahlensysteme entstehen immer dann, wenn die gegeben Zahlensysteme nicht mehr ausreichen. Nachdem man damals die natürlichen Zahlen “erfunden” hatte, um gewissen Dinge abzählen zu können, brauchte man irgendwann zum Beispiel auch mal ein neues Zahlensystem, um “ungerade” Anteile an Dingen zu messen. So sind die Brüche, also die rationalen Zahlen entstanden. Spätestens als man den Flächeninhalt eines Kreises bestimmen wollte merkte man, dass auch die rationalen Zahlen nicht mehr ausreichen (schließlich ist $\pi$ keine rationale Zahl) und die reellen Zahlen waren erschaffen (oder “entdeckt”, wie auch immer man das sehen möchte ;-).

Eine Erweiterung der reellen Zahlen

Genauso ist es bei folgendem Problem. Sagen wir, wir wollen $f(x) = x^2$ bestimmen, und zwar für alle Punkte, die die Bedingung $ x^2 + 1 = 0 $ erfüllen.

Diese Gleichung $ x^2 + 1 = 0 $ hätte die beiden Lösungen $x_1= \sqrt{-1}$ und $x_2 = -\sqrt{-1}$, wenn es denn solche Zahlen gäbe, aber wir können ja keine Wurzel aus einer negativen Zahl ziehen. Nun macht es dann auch wenig Sinn, hier weiter zu machen, aber tatsächlich würden wir ja, wenn wir diese beiden Lösungen in $f$ einsetzen würden, mit $f(x_1) = (\sqrt{-1})^2 = -1$ wieder reelle Zahlen erhalten und alles wäre wunderbar.

Tatsächlich aber ist uns das verboten, eben weil $\sqrt{-1}$ einfach nicht existiert. Und hier kommen die komplexen Zahlen ins Spiel. Sie geben uns eine Lösung, indem sie die Zahl $\sqrt{-1}$ als $\mbox{i}$ definieren. Die Lösungen zu obiger Gleichung wären also $\pm \mbox{i}$ und wir könnten damit einfach weiter rechnen und erhielten $f(x_1) = \mbox{i}^2 = -1$.

Das ist natürlich ein völlig unnützes Beispiel, aber tatsächlich gibt es Anwendungen, wo diese “nicht-existenten” Zahlen als Zwischenergebnis auftreten, und später aber durch Quadrieren wieder völlig reelle Lösungen ergeben. Aus diesem Grund hat man die Idee der komplexen Zahlen behalten, weiterentwickelt, und schließlich noch viel wichtigere Anwendungen dafür gefunden. Gerade in der Physik der Schwingungen kann man äußerst spannende Resultate mithilfe der komplexen Zahlen erreichen, weshalb zumindest jede Studentin der Ingenieurswissenschaften o.ä. die Grundlagen kennen muss.

Wie sehen komplexe Zahlen aus?

Komplexe Zahlen stellt man folgendermaßen dar

$$ z = a + \mbox{i}b $$

wobei $a, b \in \mathbb{R}$ und $\mbox{i}$ eben die imaginäre Einheit ist. Dabei nennt man $a$ den Realteil von $z$, und schreibt auch $Re(z)$ und $b$ den Imaginärteil von $z$, bezeichnet mit $Im(z)$. Sie sind also eine Kombination als reellen Zahlen und imaginären Zahlen, wenn man so will. Offensichtlich sind die komplexen Zahlen mit $b=0$, also mit Imaginärteil $=0$ gerade die reellen Zahlen.

Grafische Darstellung

Um eine solche Zahl grafisch darzustellen nimmt man die so genannte “Gaußsche Zahlenebene” oder auch “Komplexe Zahlenebene”. Im Wesentlichen hat man wie beim $\mathbb{R}^2$ zwei Achsen, wobei aber die eine den Real- und die andere den Imaginärteil abbildet. Den Imaginärteil bildet man immer auf der $y$-Achse ab. Man nennt die Achsen daher auch reelle Achse und imaginäre Achse. Im Wesentlichen ist es also nichts anderes als einen Punkt im $\mathbb{R}^2$ darzustellen und sieht dann folgendermaßen aus:

Polarform / Exponentialform

Wir kennen bereits das Konzept von Polarkoordinaten (siehe Artikel hier). Damit können wir Punkte in der Ebene anhand ihres Winkels und Abstands zum Ursprung beschreiben. Und bei den komplexen Zahlen kann uns das einiges unglaublich viel einfacher machen! Für eine Zahl $z=a+\mbox{i}b$ ergibt sich der Abstand zum Ursprung ganz “normal” mit dem Betrag:

$$ r = | z | = \sqrt{a^2 + b^2} $$

Bei $\varphi$ ist es wegen unserer imaginären Einheit $\mbox{i}$ nun ein bisschen anders (und besser!) als bei den rellen Zahlen, wir haben:

$$ a = r \cos(\varphi), ~~~ b = r\sin(\varphi) $$

Und dementsprechend

$$ z = r \cos(\varphi) + \mbox{i} r\sin(\varphi) $$

Hierbei berechnen wir $\varphi$ wieder ganz normal, mithilfe von $a$ und $b$ anstatt $x$ und $y$, wie bei normalen Polarkoordinaten. Siehe dazu auch den Artikel zu Polarkoordinaten.

Wichtig dabei: Man einigt sich bei komplexen Zahlen darauf, dass man den Winkel immer im Intervall $[-\pi, \pi)$ angibt. Dazu findet ihr unten noch ein Beispiel.

Die Eulersche Formel

Der schlaue Leonhard Euler hat nun herausgefunden, dass für jede reelle Zahl $x$ die Eulersche Formel gilt:

$$ e^{ix} = \cos(x) +  \mbox{i} \sin(x) $$

Das heißt, wir können unsere komplexe Zahl in Polarform auch noch viel schöner schreiben, nämlich so:

$$ z = r \cos(\varphi) + \mbox{i} r\sin(\varphi) = r e^{i\varphi} $$

Und das ist – zum Beispiel für Multiplikationen – unglaublich praktisch, siehe weiter unten! Danke, Leonhard!

$z = 3 + 3\mbox{i}$  wird dann zu $ z = \sqrt{18}e^{i \frac{\pi}{4}}$:

Übrigens, aus dem speziellen Fall $x=\pi$ in der Eulerschen Formel erhalten wir $ e^{i\pi} = \cos(\pi) + \mbox{i}\sin(\pi) = -1 $ und können das noch einmal umformen in diiieeeeee (Trommelwirbel):

Die schönste Formel der Mathematik!

$$ e^{i\pi} + 1 = 0 $$

Denn sie verknüpft die 5 allerwichtigsten Zahlen der Mathematik zu einer einfachen Formel!

Wie rechnet man mit komplexen Zahlen?

Ich möchte jetzt noch ein wenig auf verschiedene Rechenoperationen eingehen und dann noch zeigen, wie das anschaulich aussieht. Im Wesentlichen rechnet man mit den komplexen Zahlen genau so, wie mit reellen Zahlen, wobei man $\mbox{i}$ wie eine Variable behandelt und $\mbox{i}^2$ mit $-1$ ersetzen kann. Man bringt die berechnete Zahl dann wieder auf die Standardform $(\cdots) + \mbox{i}(\cdots)$. Das heißt:

• Addition: $ (a + \mbox{i}b) + (c + \mbox{i}d) = a + \mbox{i}b + c + \mbox{i}d = (a+c) + \mbox{i}(b+d) $ (Subtraktion genauso)
• Multiplikation: $ (a + \mbox{i}b)(c+\mbox{i}d) = a\cdot c + a\cdot \mbox{i}d + \mbox{i}b\cdot c + \mbox{i}b \cdot \mbox{i}d = ac + \mbox{i}(ad + bc) + \mbox{i}^2bd = (ac – bd) +\mbox{i}(ad + bc) $

Übrigens: Es gibt ein cooles online Tool, um sich das Ergebnis der Multiplikation darstellen zu lassen, klick hier

Multiplikation geht einfacher in Polarform!

Für die Multiplikation ergibt sich nun durch die Polarform eine extreme Erleichterung. $z$ und $w$ in Polarform sind $ z = r e^{i\varphi}$ und $ w = s e^{i{\psi}}$ und wir erhalten bei Multiplikation:

$$ z\cdot w = r e^{i\varphi} \cdot s e^{i\psi} = rs e^{i(\varphi + \psi)} $$

Also eine Addition der Winkel und eine Multiplikation der Beträge. Das sehen wir weiter unten auch nochmal am graphischen Beispiel.

Wenn ihr zwei komplexe Zahlen multiplizieren müsst, lohnt es sich sehr oft, die Zahlen vorher in Polarform zu bringen!

Zusätzlich gibt es noch eine wichtige weitere Operation, die es nur für komplexe Zahlen gibt, nämlich die komplexe Konjugation, wo man einfach das Vorzeichen des Imaginärteils umdreht:

$$ \overline{z} = \overline{(a+\mbox{i}b)} = (a -\mbox{i}b) $$

Diese erweist sich, wie wir auch weiter unten sehen werden, oft als hilfreich.

Grafische Darstellung von Operationen mit komplexen Zahlen

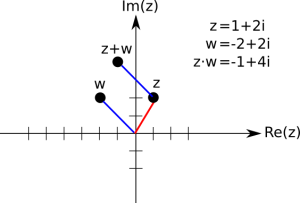
Einige Operationen haben sehr anschauliche Bedeutungen, die ich hier zeigen möchte. Nehmen wir dazu zwei Zahlen $z=1+2\mbox{i}$ und $w=-2+2\mbox{i}$.

Addition

Bei der Addition machen wir es wie bei Vektoren im $\mathbb{R}^2$ und addieren die Koeffizienten. Wir fassen zwei komplexe Zahlen $a+ib$ und $c+id$ als Vektoren $(a,b)$ und $(c,d)$ auf und addieren diese einfach. Wir bekommen also $(a+c, b+d)$ und wie im $\mathbb{R}^2$ haben wir eine “Hintereinanderschaltung” von Vektoren, siehe folgendes Bild. In unserem Beispiel also ist $z+w = 1+2i + (-2) + 2i = -1 + 4i$.

Multiplikation

Die Multiplikation ist besonders interessant: Eine Multiplikation von zwei komplexen Zahlen entspricht einer Drehung und Streckung in der komplexen Ebene. Beim Multiplizieren denken wir uns einfach $i$ wieder als Variable und multiplizieren die einzelnen Koeffizienten, wobei wir dann $i^2$ immer mit $-1$ ersetzen können: $ z \cdot w = -2 + 2i – 4i +4i^2 = -2 -2i – 4 = -6 -2i $

Bei der Multiplikation multipliziert sich auch der Betrag: $|z| = \sqrt{5}$, $|w| = \sqrt{8}$ und $|zw| = \sqrt{36+4} = \sqrt{40} = \sqrt{8}\sqrt{5}$. Das ist generell eine Eigenschaft der Betragsfunktion, nicht nur bei komplexen Zahlen! Für Beträge gilt immer $|a||b| = |ab|$, auch bei z.B. reellen Zahlen.

Multiplikation in Exponentialform / Polarform

Aber viel klarer wir das, wenn wir hierfür die Polarform bzw. Exponentialform benutzen! Dann ist $ z= \sqrt{5} e^{0.35\pi i}$ und $w = \sqrt{8} e^{0.75 \pi i}$, also $z \cdot w = (\sqrt{5} e^{0.35\pi i}) \cdot (\sqrt{8} e^{0.75 \pi i}) = \sqrt{5}\sqrt{8} e^{0.35\pi i + 0.75\pi i} = \sqrt{40}e^{1.1\pi i }$. Vorsicht! Diese Aussage ist zwar richtig, aber wir wollen den Winkel eigentlich immer nur im Bereich $[-\pi, \pi)$ angeben. Der Winkel, den wir hier haben, beträgt $1.1\pi$, gemessen gegen den Uhrzeigersinn von der x-Achse aus, wie im Bild oben gezeigt (grüner Pfeil). Tatsächlich aber wollen wir für solche Winkel, die größer als $\pi$ (also größer als $180°$) sind, andersherum messen, siehe Bild unten. Dafür ziehen wir einfach $2\pi$ von unserem “zu großen” Winkel ab und erhalten $1.1\pi – 2\pi = -0.9\pi$.

Abschließend können wir die Aussagen über die Multiplikation mit Exponentialform nochmal nachprüfen, indem wir die Polarform von $-6 – 2i$ bilden: Für den Betrag bekommen wir $\sqrt{36 + 4} = \sqrt{40}$ und für den Winkel $- \arccos(\frac{-6}{\sqrt{40}}) \approx -0.9\pi $, also genau das, was wir wollten.

Komplexe Konjugation

Die komplexe Konjugation ist einfach eine Spiegelung an der reellen Achse, schließlich bleibt der Realteil derselbe, und der Imaginärteil wechselt das Vorzeichen.

Eigenschaften

Die komplexen Zahlen bilden einen Körper

Die komplexen Zahlen $\mathbb{C}$ bilden einen Körper (siehe Artikel Gruppen, Ringe und Körper), denn sie erfüllen alle nötigen Kriterien dafür. Ohne das jetzt hier formal zu zeigen, sollte einleuchten, dass die Dinge wie Multiplikation und Addition auf den komplexen Zahlen “ganz normal” funktionieren. Für die Körpereigenschaft muss auch die Kommutativität der Verknüpfungen gewährleistet sein, für die Addition ist das offensichtlich, aber es gilt auch für die Multiplikativität:

$$ (a + \mbox{i}b)(c+\mbox{i}d) = a\cdot c + a\cdot \mbox{i}d + \mbox{i}b\cdot c + \mbox{i}b \cdot \mbox{i}d = ac + \mbox{i}(ad + bc) + \mbox{i}^2bd = (ac – bd) + \mbox{i}(ad + bc) $$

Und

$$ (c+\mbox{i}d)(a + \mbox{i}b) = ca + c\mbox{i}b + \mbox{i}da + \mbox{i}^2db = (ac – bd) + \mbox{i}(ad + bc) $$

Etwas interessanter wird es bei der Frage bezüglich des Inversen. Für die Addition ist das offensichtlich auch gegeben, aber wie sieht es mit der Multiplikation aus? Nehmen wir also mal eine komplexe Zahl $z = a + \mbox{i}b$ mit $a\neq 0$ und $b\neq 0$. Dann müssen wir eine weitere Zahl $w = c+\mbox{i}d$ finden, sodass $z\cdot w = 1_\mathbb{C}$. Hierbei ist eben das Einselement $1_\mathbb{C}$ das Element $1 + i0$ also einfach die reelle Zahl $1$. Um zu zeigen, dass ein solches Inverses existiert müssen wir in die Trickkiste greifen und einen Trick anwenden, den wir bei komplexen Zahlen sehr häufig benutzen können, also merken!

Der Trick ist, mit einem Bruch zu erweitern, der in Zähler und Nenner die komplexe Konjugation enthält:

$$ \begin{align} z\cdot z^{-1} &= 1 \\ \Leftrightarrow z^{-1} &= \frac{1}{z} \\  &= \frac{1}{z} \cdot \frac{\overline{z}}{\overline{z}} \\ &=  \frac{1}{a+ib} \cdot \frac{\overline{a+ib}}{\overline{a+ib}} = \frac{1}{a+ib} \cdot \frac{a-ib}{a-ib} = \frac{a-ib}{a^2 + b^2} = \frac{a}{a^2 + b^2} + i\frac{-b}{a^2 + b^2} \\  &=  \frac{a}{a^2 + b^2} + i\frac{-b}{a^2 + b^2} \end{align} $$

Wir haben also hiermit für jedes $ z \in \mathbb{C} $ ein inverses Element $ z^{-1} $ gefunden.

Die komplexen Zahlen bilden einen Vektorraum

Wenn man die Zahlen $ z = a + \mbox{i}b $ als Vektoren $(a,b)$ auffasst, so ist das ein Vektorraum. $ \mathbb{C} $ ist also ein Vektorraum.

Der Fundamentalsatz der Algebra

Über den komplexen Zahlen hat jedes Polynom eine Nullstelle! Das heißt auch, dass jede algebraische Gleichung (also eine Gleichung mit Polynomen) eine Lösung hat! Das ist in den reellen Zahlen nicht so (siehe Beispiel in der Einleitung) und eine der wichtigsten Eigenschaften der komplexen Zahlen und warum man so gut mit ihnen rechnen kann.

Weiterführende Artikel:

Polarkoordinaten

Vektorräume (in Arbeit)