Die injektive/ surjektive/ bijektive Kneipenprügelei

Die drei Eigenschaften Injektivität, Surjektivität und Bijektivität beziehen sich auf Abbildungen (Funktionen) zwischen zwei Mengen und führen oft zu Verwirrung. Ich möchte diese Eigenschaften hier an dem naheliegenden Beispiel einer Prügelei erklären, um diese Verwirrung hoffentlich beseitigen zu können. Schauen wir uns zunächst aber einmal die mathematischen Definitionen an.

Eine Funktion $f:X\rightarrow Y$

• heißt injektiv, wenn gilt: $f(x_1)=f(x_2) \Rightarrow x_1=x_2$, will heißen: für jedes $y\in Y$ gibt es entweder nur ein $x\in X$, für das $f(x)=y$ gilt, oder gar keins. Aber niemals mehrere $x$, die den gleichen Funktionswert haben.
• heißt surjektiv, wenn gilt: Für alle $y\in Y$ existiert mindestens ein $x\in X$, sodass $f(x)=y$ gilt. Heißt also, dass jedes $y$ von mindestens einem $x$ erreicht wird, möglicherweise auch von mehreren.
• heißt bijektiv, wenn sie surjektiv und bijektiv zugleich ist. Das heißt also dass jedes $x$ genau auf ein $y$ abbildet, kein $y$ doppelt getroffen wird und kein $y$ ausgelassen wird.

Die injektive/surjektive/bijektive Kneipenprügelei

Stellen wir uns nun eine Kneipe vor, in dem sich einige Herren (wir erinnern uns, die Herren der Schöpfung haben im Gegensatz zu den Damen ein $Y$-Chromosom!) feucht-fröhlich amüsieren. Es kommt eine Gruppe weiblicher Amazonen (mit $X$-Chromosomen) daher, die ziemlich auf Krawall gebürstet ist. Nach einigen frechen Sprüchen seitens der Herren eskaliert die Situation, und die Amazonen verprügeln die Männer.

Wat hat dat denn mit Mathe zu tun? Naja, die Amazonen sind unsere Menge X, die Kerle die Menge Y. Und wann immer eine Amazone x einem Kerl y eine reinhaut, haben wir eine Funktion von X nach Y. Damit das ganze auch wirklich eine Funktion ist (wir erinnern uns, bei einer Funktion wird einem x höchstens ein y zugewiesen), nehmen wir an, dass jede Amazone jeweils maximal einem Mann eine reinhaut.

Es gibt nun drei Möglichkeiten, wie es ablaufen könnte:

Injektiv

Injektiv heißt anschaulich: Jedem y-Wert wird maximal ein x-Wert zugeordnet! Bei unserer Prügelei heißt das, dass niemals zwei Amazonen auf einen Mann gehen würden. Dann gäbe es nämlich zwei x-Werte, die auf einen y-Wert abbilden. Das wäre nicht injektiv! Das heißt aber nicht, dass auch alle Männer etwas abkriegen. Helmut zum Beispiel hat direkt Angst bekommen und sich hinter der Theke versteckt, er kriegt keine rein, es gibt also kein x, welches auf den speziellen y-Wert “Helmut” abgebildet wird. Ist aber egal, trotzdem injektiv!

Surjektiv

Surjektiv ist die Schlägerei, wenn wirklich jeder Mann eine reinkriegt. Das heißt nämlich, dass für jeden y-Wert mindestens ein x da ist, um auf diesen y-Wert abzubilden. Wenn wie vorher tatsächlich Helmut hinter der Bar versteckt bleibt, ist unsere Schlägerei nicht surjektiv, denn dann wäre Helmut genau der y-Wert, der von gar keinem x erreicht wird. Hier lässt sich auch eine spezielle Sache der Surjektivität erklären: Angenommen, Helmut wäre gar nicht da, unsere $Y$-Menge also um 1 kleiner, ansonsten aber keinerlei Änderung beim Kampf: Dann wäre die Schlägerei surjektiv, denn außer Helmut kriegen alle etwas ab. Das heißt: Surjektivität hängt ganz besonders von der Y-Menge ab: Wir können die Funktion gleich lassen (an der Schlägerei an sich ändert sich nichts), machen unsere Menge Y aber etwas kleiner und alle y-Werte werden getroffen: Die Funktion, die vorher nicht surjektiv war, ist es nun.

Bijektiv

Bijektiv ist die Rauferei, wenn wirklich jede Amazone genau einen Mann verkloppt und auch kein Mann seinem Schicksal entgeht, also jeder etwas abbekommt. Es gibt also eine 1-zu-1-Beziehung, wiklich jede Amazone haut genau einen Mann und niemand bleibt übrig. Die Abbildung ist damit injektiv (jeder Mann bekommt von maximal einer Amazone etwas ab) und surjektiv (ohne Ausnahme bekommt jeder Mann etwas ab). Das heißt insbesondere: Die Funktion ist umkehrbar! Die Männer, die nun ordentlich eingesteckt haben, drehen den Spieß um, und verprügeln die Amazonen, und zwar ein jeder genau die, von der er eine abbekommen hat! Y bildet nun auf X ab und natürlich wieder 1-zu-1.

Nachdem die Kerle nun also die Frauen zurückgehauen haben, einigte man sich darauf, dass das ganze mit dem Prügeln doch irgendwie Schwachsinn ist und entschloss sich, lieber ein paar Biere zu trinken. Danach ging man gemeinsam nach Hause um Liebe zu machen. Ob das immernoch bijektiv war, oder vielleicht doch mehrere x auf ein y kamen, weiß ich nicht mehr. 😉

Zurück zur Mathematik: Beispiele!

Jetzt wollen wir noch ein paar mathematische Beispiele durchgehen! Danach könnt ihr auch gerne in die Kneipe gehen.

Beispiel 1

$$ f : \mathbb{R} \rightarrow \mathbb{R},~~ f(x) = x^2 $$

ist als solches weder injektiv noch surjektiv! Denn alle y-Werte außer Null werden von zwei x-Werten erreicht (also nicht injektiv) und manche y-Werte werden gar nicht erreicht, alle negativen Zahlen nämlich (also nicht surjektiv). Letzteres können wir aber ändern, indem wir den tatsächlichen minimalen Wertebereich von f nehmen (nennt man auch Bild(f)):

$$ f : \mathbb{R} \rightarrow \mathbb{R}_{\geq 0},~~ f(x) = x^2 $$

Jetzt ist die Funktion surjektiv (jedes $y \in \mathbb{R}_{\geq 0}$ wird erreicht), obwohl wir eigentlich gar nichts geändert haben: wenn wir die Funktion zeichnen würden, würde sie immernoch genauso aussehen wie vorher!

Damit die Funktion injektiv wäre, müssten wir ihren Definitionsbereich einschränken, zum Beispiel nur alle x-Werte zulassen, die größer oder gleich Null sind. Beachtet, dass wir dann eine wirkliche Änderung an der Funktion machen, die sieht nämlich dann nur noch so aus:

Die Funktion

$$ f : \mathbb{R}_{\geq 0} \rightarrow \mathbb{R}_{\geq 0},~~ f(x) = x^2 $$

ist also sowohl injektiv, als auch surjektiv, also bijektiv. Die Umkehrfunktion kennen wir alle, sie lautet:

$$ f^{-1} : \mathbb{R}_{\geq 0} \rightarrow \mathbb{R}_{\geq 0},~~ f^{-1}(x) = \sqrt{x} $$

Wir sehen: Der Definitionsbereich von $f$ wird zum Wertebereich von $f^{-1}$ und umgekehrt!

Beispiel 2

$$ f : \mathbb{R} \rightarrow \mathbb{R},~~ f(x) = e^x $$

ist als solche injektiv, aber nicht surjektiv. Wenn wir allerdings den Wertebereich auf $\mathbb{R}_{> 0}$ ändern, welches absolut nichts ändert, ist die Funktion bijektiv mit Umkehrfunktion

$$ f^{-1} : \mathbb{R}_{>0} \rightarrow \mathbb{R},~~ f^{-1}(x) = \ln(x) $$

wieder ist der Definitionsbereich von $f$ der Wertebereich von $f^{-1}$, und der (eingeschränkte) Wertebereich von $f$ ider der Definitionsbereich von $f^{-1}$.

Beispiel 3

$$ f : \mathbb{R} \rightarrow \mathbb{R},~~ f(x) = 5 $$

ist weder surjektiv noch injektiv.

Beispiel 4

$$ f : \mathbb{R} \rightarrow \mathbb{R},~~ f(x) = \sin(x) $$

ist weder surjektiv noch injektiv, das kann man sich am Graphen veranschaulichen:

Der Sinus kann aber surjektiv gemacht werden indem wir (keine Änderung an der Funktion, sähe immernoch genauso aus) den Wertebereich einschränken:

$$ f : \mathbb{R} \rightarrow [-1; 1],~~ f(x) = \sin(x) $$

Für Bijektivität müssten wir die Funktion tatsächlich verkleinern, z.B. ist:

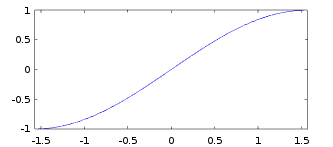
$$ f : [-\frac{\pi}{2}; \frac{\pi}{2}] \rightarrow [-1; 1],~~ f(x) = \sin(x) $$

bijektiv:

Hinweise

Die Einschränkung des Definitionsbereich ist wie oben beschrieben und an x² gezeigt, wirklich eine Veränderung der Funktion. Deshalb schreibt man dies auch oft explizit hin, z.B. so:

$$ f|_{ [-\frac{\pi}{2}; \frac{\pi}{2}]} $$

Damit klar ist, dass es um die Einschränkung geht.